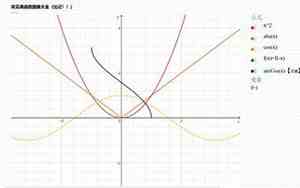
奇函数和偶函数是数学中函数分类的两个重要概念，它们在数学分析中扮演着关键角色。
奇函数：
1. 定义：如果函数\( f(x) \)满足对于定义域内的任何\( x \)，都有\( f(-x) = -f(x) \)，则称\( f(x) \)为奇函数。
2. 性质高亮：
它的图像关于原点对称：\( f(x) \)的图像与原点连线的垂线相交的所有点，其像点都是函数值的相反数。
奇函数的原点处有特殊性质：\( f(0) = 0 \)（除了常数零函数）。
奇函数的积分结果为零：对所有实数区间，\( \int_{-a}^{a} f(x) \，dx = 0 \)。
偶函数：
1. 定义：如果函数\( f(x) \)满足\( f(-x) = f(x) \)，则\( f(x) \)为偶函数。
2. 性质高亮：
它的图像关于y轴对称：所有点关于y轴的对称点都在函数图象上。
偶函数的轴对称性：\( f(x) = f(-x) \)，在y轴上的点处函数值保持不变。
对于定义域包含0的偶函数，\( f(0) \)是其值域中的一个常数。
奇函数和偶函数的性质主要体现在对称性和特殊点的函数值上，这对于理解和解决相关数学问题具有重要作用。
判断一个函数是否为奇函数或偶函数，主要有以下两种方法：
奇函数判断：
如果对于定义域中的任意\( x \)，都有\( f(-x) = -f(x) \)，则函数\( f(x) \)是奇函数。
举个例子，假设\( f(x) = x^3 \)，那么\( f(-x) = (-x)^3 = -x^3 = -f(x) \)，所以\( f(x) \)是奇函数。
偶函数判断：
如果对于定义域中的任意\( x \)，都有\( f(-x) = f(x) \)，则函数\( f(x) \)是偶函数。
例如，\( f(x) = x^2 \)，那么\( f(-x) = (-x)^2 = x^2 = f(x) \)，所以\( f(x) \)是偶函数。
奇函数：观察函数的图像，如果图像关于原点中心对称，且在原点处的值为0（除了常数0函数），则为奇函数。
偶函数：图像关于y轴对称，无论x取何值，图像上方的部分与下方的部分完全对称。
通过以上验证，你可以确定一个函数是否满足奇函数或偶函数的定义，从而进行分类。
理解奇偶函数的加减乘除关系，可以通过以下口诀来记忆：
两个奇函数相加，结果是奇函数。
两个奇函数相减，结果同样是奇函数。
一个奇函数加一个偶函数，结果是奇函数。
一个奇函数减一个偶函数，结果是偶函数。
两个奇函数相乘，结果是奇函数。
奇函数除以奇函数（非零），结果是奇函数。
两个偶函数相加，结果是偶函数。
两个偶函数相减，结果还是偶函数。
一个奇函数乘以一个偶函数，结果是偶函数。
偶函数除以偶函数（非零），结果是偶函数。
注意，这些规则仅适用于函数在其定义域内的乘法和除法。对于乘法，如果除数为0，函数定义可能需要重新考虑，因为奇函数除以0在数学上没有定义。同样，对于除法，被除数必须是非零奇函数或偶函数。
奇函数和偶函数的运算法则如下：
1. 加法：
2. 减法：
3. 乘法：
奇函数 * 偶函数 = 偶函数 （结果是乘积函数，也可以看作是奇偶性互为相反）
4. 除法（前提：除数非零）：
奇函数 / 偶函数（非零） = 奇函数 / 偶函数 = 奇函数 （除数为奇函数，奇函数除以偶函数仍然是奇函数）
这些规则是根据奇函数和偶函数的定义以及乘法分配律得出的。在操作时，如果遇到分母为奇函数的情况，要小心，因为奇除奇等于奇，但如果除数是偶函数，结果则保持奇函数的性质。
奇函数和偶函数的加减乘除运算是根据它们各自的定义和性质来计算的。以下是基本规则：
奇函数 * 偶函数 = 偶函数 （因为奇数乘偶数是偶数）
奇函数 / 奇函数 = 奇函数 （奇数除以奇数仍然是奇数）
奇函数 / 偶函数（非零） = 奇函数 （奇数除以偶数仍为奇数，前提是非零除数）
记住，这些规则是在函数在其定义域内适用的。如果遇到乘除两端的函数中包含不明显的奇偶性，通常要考虑它们的具体形式。例如，对于奇函数\( f(x) \)和偶函数\( g(x) \)，\( f(x) \cdot g(x) \)的结果取决于\( f(x) \)和\( g(x) \)的具体形式。如果\( f(x) \)是偶数倍的奇数，那么\( f(x) \cdot g(x) \)将是偶数。
奇函数和偶函数关于以下对称性：
1. 奇函数：
奇函数的图像关于原点（\( (0，0) \)）对称。也就是说，如果点\( (x， y) \)在奇函数图象上，那么对应的点\( (-x， -y) \)也在图象上。
这意味着如果\( f(x) \)是奇函数，则\( f(-x) = -f(x) \)，这使得函数的x轴对称。
2. 偶函数：
偶函数的图像关于y轴（\( x = 0 \)）对称。任何点\( (x， y) \)在偶函数图象上，其关于y轴对称的点\( (-x， y) \)也在图象上。
所以，如果\( f(x) \)是偶函数，则\( f(-x) = f(x) \)，这使得函数的y轴对称。
总结来说，奇函数的对称性是关于原点的，而偶函数的对称性是关于y轴的。这是由它们各自的定义所决定的。
奇函数和偶函数的性质通常体现在它们的图像和函数值上：
奇函数：
图像：奇函数的图像关于原点对称。在原点（\( x = 0 \)）处，函数值为0，非零点关于原点成对出现（\( f(x) \)和\( f(-x) \)关于原点对称）。
性质：奇函数满足\( f(-x) = -f(x) \)，这意味着奇函数关于y轴是不对称的，但关于原点是对称的。
偶函数：
图像：偶函数的图像关于y轴对称。所有点关于y轴的对称点都在图象上，且函数值在\( x \)轴两侧是对称的（\( f(x) = f(-x) \)）。
性质：偶函数满足\( f(-x) = f(x) \)，表示其在y轴两侧的值是相同的。
奇函数的典型例子如\( f(x) = x^3 \)和\( f(x) = \sin x \)，偶函数的典型例子如\( f(x) = x^2 \)和\( f(x) = \cos x \)。
总结来说，奇函数和偶函数的性质不仅体现在它们的函数定义，还体现在它们的图形特性上，这也是一些函数容易识别的原因。
猜你喜欢
