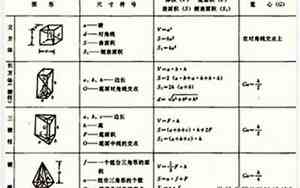
三棱柱是一种具有三个侧面的柱状立体，每个侧面都是一个三角形。要计算三棱柱的体积，需要知道三个关键参数：底面面积和高。
一个三棱柱的体积 \( V \) 可以通过底面积 \( A \) 乘以高 \( h \) 计算得出，公式如下：
\[
V = A \times h
\]
其中，底面积 \( A \) 通常指的是底面三角形的面积，公式为：
如果底面是等腰三角形（底边和高都相等），那么：
\[
A = \frac{1}{2} \times \text{底边长} \times \text{高}
\]
如果底面是任意三角形，需要知道底边长 \( b \) 和对应高 \( h_1 \)（即从一个顶点垂直于底面的线段）：
\[
A = \frac{1}{2} \times b \times h_1
\]
高 \( h \) 是从底面到底面的垂直距离。
所以，要计算三棱柱的体积，你只需要知道底面积和高，将它们代入体积公式中即可得到结果。注意，如果提供的是底边和两个对应边的高（对于非等腰三角形），则需要根据具体情况转换为底边和高来计算面积。
三棱柱的体积公式是通过几何直观和体积积分的概念来推导的。我们先假设三棱柱的底面是一个三角形，高是垂直于底面的线段。下面是一种直观的思考：
1. 直观理解：
假设有一个三棱柱，你可以想象将它切割成许多极小的立方体，每个立方体的体积是 \( \Delta V \)，当高度 \( h \) 越来越小，这些立方体接近于一个无限小的连续体，然后它们的体积之和就构成了整个三棱柱的体积。
2. 体积微分：
取每个小立方体的体积为 \( \text{width} \times \text{height} \times \text{depth} \)。在一个非常小的高度变化 \( \Delta h \) 下，宽度和深度保持不变，所以每个小立方体的体积近似为 \( A \Delta h \)，其中 \( A \) 是底面的面积。
3. 积分求和：
当 \( \Delta h \) 趋近于0，这些小立方体的体积之和就形成一个积分。如果我们把所有这些小立方体的体积加起来，就得到了三棱柱的体积 \( V \)：
\[
V = \lim_{\Delta h \to 0} \sum_{i=1}^{n} A \Delta h = \int_{0}^{h} A dh
\]
4. 公式得出：
体积积分的形式简化为：
\[
V = A \times h
\]
这就是三棱柱体积的基本公式，其中 \( A \) 是底面面积，\( h \) 是三棱柱的高。
这个推导过程虽然较为抽象，但它是通过从大量微小体积的堆积中得出的，因此是准确的。
三棱柱的体积计算公式非常直接，它是基于底面积 \( A \) 和高 \( h \) 的乘积来计算的。如果三棱柱的底面是一个等腰三角形，底边长 \( b \) 和高 \( h \) 相等，那么体积 \( V \) 计算如下：
\[
V = \frac{1}{2} \times b \times h \times h = \frac{1}{2}bh^2
\]
如果底面是任意三角形，底边长为 \( b \)，高为 \( h_1 \)（垂直于底面的高），则底面积 \( A \) 用 \( \frac{1}{2}bh_1 \) 来计算，体积则为：
\[
V = \frac{1}{2}b \times h_1 \times h
\]
这里的 \( h \) 是三棱柱从底面到底面的垂直高度。所以，要计算三棱柱的体积，你需要知道底边长、高（如果底面是等腰三角形）或底面的高和底面的长度，以及垂直高度。将这些数值代入相应的公式即可得到体积。
三棱柱的体积和表面积公式如下：
1. 体积 \( V \)：
如果三棱柱的底面是等腰三角形，底边长 \( b \) 和高 \( h \) 相等，那么体积 \( V \) 计算为：
\[
V = \frac{1}{2}bh^2
\]
如果底面是任意三角形，底边长 \( b \) 和高 \( h_1 \)：
\[
V = \frac{1}{2}b \times h_1 \times h
\]
其中 \( h \) 是三棱柱的垂直高度。
2. 表面积 \( A \)：
三棱柱的表面积包括两个底面面积和三个侧面积。如果底面是等腰三角形，那么：
底面面积 \( A_{base} = 2 \times \frac{1}{2}bh = b \times h \)（由于有两个底面，乘以2）
侧面积 \( A_{lateral} \) 是三个等腰三角形侧面的面积之和，因为每个侧面面积 \( A_{side} = \frac{1}{2}bh \)，所以：
\[
A_{lateral} = 3 \times \frac{1}{2}bh = \frac{3}{2}bh
\]
表面积 \( A \) 就是底面面积和侧面积之和：
\[
A = A_{base} + A_{lateral} = b \times h + \frac{3}{2}bh
\]
如果底面是任意三角形，侧面积的计算方法是相同的。
总表面积 \( A \) 则是两个底面和三个侧面的面积之和，不必考虑底面是等腰还是任意三角形。
三棱柱的体积公式是基于其底面积 \( A \) 和高度 \( h \) 来计算的。如果三棱柱的底面是等腰三角形，底边长 \( b \) 和高 \( h \) 相等，体积 \( V \) 为：
\[
V = \frac{1}{2}bh^2
\]
如果底面是任意三角形，且已知底边长 \( b \) 和垂直于底边的高 \( h_1 \)，体积 \( V \) 为：
\[
V = \frac{1}{2}b \times h_1 \times h
\]
在这个公式中，\( h \) 是三棱柱从底面到底面的垂直高度。记得，底面三角形的面积需要根据实际情况来计算。
三棱柱体积的图解通常是这样的：
1. 图形描绘：
三棱柱是一个上底与下底都是三角形，中间被一个侧面（也可能是三个侧面，但这里通常是上面和下面各一个）连接的长方体。底面的两个三角形是相同的，它们被等腰或非等腰三角形描述。
2. 体积形成：
为了计算体积，你可以想象三棱柱是由很多非常小的立方体（体积为 \( \Delta V \) 的微小块）堆叠起来形成的。当这些微小立方体的体积积少成多时，就形成了三棱柱的总体积。
3. 体积计算：
如果底面是等腰三角形，每个微小立方体的体积是 \( \frac{1}{2} \text{底边长} \times \text{高} \times \text{高度变化} \)。当高度变化无穷小时，积分计算的体积就是 \( \frac{1}{2} \text{底边长} \times \text{高}^2 \)。
如果底面是任意三角形，计算类似，但需要使用底边 \( b \) 和垂直于底面的高 \( h_1 \)。
4. 公式直观：
这种图形帮助我们理解体积公式，即底面积（三角形面积）乘以高度。因此，体积公式可以直观地写为 \( V = A \times h \)，其中 \( A \) 是底面积。
通过这个图解，你可以形象地理解三棱柱体积的计算过程。
三棱柱的体积之所以是底面积乘以高，是因为体积本质上是立体空间所占的量，而底面积是这个空间底部的投影面积，高则是垂直于底面的距离，代表了从底面到底面的占用空间。
想象一下，三棱柱是由无数个小正方体堆积起来的，每个小正方体的体积就是底面积乘以高的乘积。当这些小正方体叠在一起形成三棱柱时，所有小正方体的体积之和就等于整个三棱柱的体积。如果我们将每个小正方体的体积简化为底面积乘以高，那么所有这些小体积加起来，就得到三棱柱的总体积，这也是体积公式 \( V = A \times h \) 的几何解释。这个公式适用于任何三棱柱，无论底面是等腰三角形还是不等腰三角形，只要提供对应的高度和底面大小即可。
猜你喜欢
