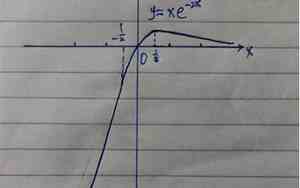
在数学中，函数的拐点是指函数曲线上的一个点，它是由凹陷向上转为凸起向上或由凸起向上转为凹陷向上的转折点。换句话说，函数的拐点是函数曲线上的一个点，在这个点处，函数的曲率（即函数曲线的弯曲程度）发生了变化。
函数的拐点在数学和物理学中都有重要的应用。例如，在物理学中，函数曲线上的拐点可以表示物体在运动中的加速度发生变化的点。在经济学中，函数曲线上的拐点可以表示生产或销售业绩的变化点。因此，理解函数的拐点对于解决各种实际问题非常重要。
函数的拐点可以通过计算函数的二阶导数来找到。二阶导数是一条曲线的斜率的斜率，也就是说，它是曲线的曲率。如果函数的二阶导数大于0，则函数在该点处是凸起向上的；如果二阶导数小于0，则函数在该点处是凹陷向上的；如果二阶导数等于0，则函数在该点处可能是一个拐点。如果函数在拐点处是凸起向上的，则拐点是函数的最小值点；如果函数在拐点处是凹陷向上的，则拐点是函数的最大值点。
函数的拐点可以帮助我们理解函数的变化趋势。例如，通过找到函数的拐点，我们可以确定函数的最大值和最小值，以及函数的增长和下降趋势。此外，在函数拐点的附近，我们可以找到函数的局部最值点，这些最值点可以帮助我们更好地理解函数的行为。
当我们研究复杂的函数时，函数的拐点可以作为我们进行进一步分析的起点。例如，在微积分中，我们可以利用函数的拐点来确定函数的极值和函数的趋势。在统计学中，我们可以利用函数的拐点来确定数据的分布形式和数据的异常点。在经济学中，我们可以利用函数的拐点来分析市场的变化趋势和企业的生产效率。
总之，函数的拐点是函数分析中很重要的一部分。通过理解函数的拐点，我们可以更好地理解函数的行为，找到函数的最值点和局部最值点，以及确定函数的变化趋势。对于数学、物理学、经济学等领域的研究者来说，掌握函数的拐点是非常重要的。
函数的拐点是指函数在某一点上的导数从正数变为负数，或者从负数变为正数的点。在拐点处，函数的曲线会发生突然转折，由凸转为凹或者由凹转为凸。函数图像在拐点处的斜率为0，因此它是函数图像的极值点之一。在求函数的最大值或最小值时，需要考虑函数的拐点。
函数的拐点是指函数图像上的一个点，它左右两侧的函数增减性发生了改变，也就是函数的导数发生了变化，此时函数图像会发生从凸向上的弯曲，变成凸向下的弯曲，或者反过来。拐点的位置是函数图像上一个非常重要的点，它能够告诉我们函数的凸性、极值和变化趋势等信息，对于函数的研究和优化具有很大的帮助。
一、函数的拐点。函数的拐点是指函数图象在该点处由弯曲向上凹或由弯曲向下凸的转折点。二、求函数拐点的一般步骤。1. 求出函数的二阶导数 $f''(x)$。2. 令 $f''(x)=0$，解得所有的驻点。3. 求出这些驻点对应的函数值 $f(x)$。4. 比较相邻两个驻点处的函数值 $f(x)$ 的大小关系，确定拐点。具体做法如下：。若 $f''(x)>0$，则函数图象在 $x$ 处由弯曲向下凸变为弯曲向上凹，$x$ 点为函数的拐点。若 $f''(x)<0$，则函数图象在 $x$ 处由弯曲向上凹变为弯曲向下凸，$x$ 点为函数的拐点。若 $f''(x)=0$，则无法确定函数是否有拐点。需要注意的是，当函数的二阶导数不存在时，也有可能产生拐点。此时需要通过极限的方法进行分析。
猜你喜欢
