向量和平面是数学中重要的概念，它们在几何、物理、工程等领域中都有着广泛的应用。向量的乘法是向量积和数量积两种形式，而平面向量的乘积则是向量积的一种具体形式。在本文中，我们将重点介绍向量和平面的乘法公式，以及平面向量的乘积公式。
一、向量的乘法。
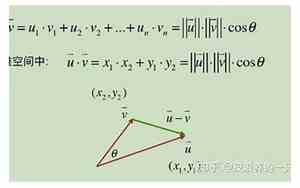
在向量的乘法中，最常见的是数量积和向量积。数量积也称点积，它的结果是一个标量，表示两个向量之间的夹角余弦值与它们的模的乘积。向量积也称叉积，它的结果是一个向量，与两个向量所在平面垂直，大小等于两个向量所在平面的面积，方向满足右手法则。
数量积公式：。
设向量a和b的夹角为θ，则它们的数量积为：。
a·b = |a||b|cosθ。
其中，|a|和|b|分别表示向量a和b的模长。
向量积公式：。
设向量a和b的夹角为θ，则它们的向量积为：。
a × b = |a||b|sinθn。
其中，n为垂直于a和b所在平面的单位向量，满足右手法则。
二、平面的乘法。
在平面的乘法中，我们主要讲述平面向量的乘积。平面向量的乘积也称为向量的外积或向量积，是向量积的一种具体形式。如果我们把平面向量看成是二维向量，那么平面向量的乘积就是向量积的结果向量在z轴上的分量。
平面向量的乘积公式：。
设平面向量a和b的坐标分别为(x1, y1)和(x2, y2)，则它们的乘积为：。
a × b = (0, 0, x1y2 - x2y1)。
其中，(0, 0)表示向量a和b所在平面的法向量，也就是z轴的方向，x1y2 - x2y1表示它们所在平面的面积。
三、总结。
向量和平面的乘法在数学和物理中有着广泛的应用，可以用来描述物体的运动、力学等问题。数量积和向量积是向量的两种乘法形式，分别表示夹角余弦值和向量所在平面的面积。平面向量的乘积是向量积的一种具体形式，可以用来计算平面上两个向量所构成的平行四边形的面积，从而得到平面向量的模长。学好向量和平面的乘法，不仅可以解决各种数学问题，还可以帮助我们更好地理解物理和工程学科中的知识。
1. 向量和平面相乘公式。向量和平面可以相乘，其结果是一个向量。设向量 $\vec{a}$ 和平面 $\Pi$，则它们的乘积可以表示为：。$$\vec{a}\times \vec{\pi}$$。其中，$\vec{\pi}$ 表示平面 $\Pi$ 的法向量。2. 三向量的基本运算。三向量的基本运算包括向量的加法、减法、数量积、向量积等。(1) 向量的加法。向量的加法指的是将两个向量相加得到一个新的向量。设 $\vec{a}$ 和 $\vec{b}$ 是两个向量，则它们的和可以表示为：。$$\vec{a}+\vec{b}=(a_1+b_1,a_2+b_2,a_3+b_3)$$。(2) 向量的减法。向量的减法指的是将一个向量减去另一个向量得到一个新的向量。设 $\vec{a}$ 和 $\vec{b}$ 是两个向量，则它们的差可以表示为：。$$\vec{a}-\vec{b}=(a_1-b_1,a_2-b_2,a_3-b_3)$$。(3) 数量积。数量积指的是将两个向量的对应分量相乘再相加得到一个标量。设 $\vec{a}$ 和 $\vec{b}$ 是两个向量，则它们的数量积可以表示为：。$$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+a_3b_3$$。(4) 向量积。向量积指的是将两个向量相乘得到一个新的向量。设 $\vec{a}$ 和 $\vec{b}$ 是两个向量，则它们的向量积可以表示为：。$$\vec{a}\times\vec{b}=\begin{pmatrix}a_2b_3-a_3b_2 \\a_3b_1-a_1b_3 \\a_1b_2-a_2b_1\end{pmatrix}$$。其中，向量 $\vec{a}\times\vec{b}$ 垂直于向量 $\vec{a}$ 和 $\vec{b}$，且其大小为 $|\vec{a}||\vec{b}|\sin{\theta}$，其中 $\theta$ 是向量 $\vec{a}$ 和 $\vec{b}$ 的夹角。
1. 向量和平面相乘公式。当一个向量与一个平面相乘时，可以通过将该向量垂直投影在该平面上，得到新的向量。具体而言，设向量 $\vec{a}$ 与平面 $\alpha$ 相乘，则：。$$\vec{a}\cdot \vec{n_{\alpha}}$$。其中，$\vec{n_{\alpha}}$ 是平面 $\alpha$ 的法向量，$\cdot$ 表示向量的点积运算。2. 平面向量的乘法运算。设有两个平面向量 $\vec{a}=(a_1,a_2)$ 和 $\vec{b}=(b_1,b_2)$，则它们的乘积（即叉积）为：。$$\vec{a}\times\vec{b}=|\vec{a}||\vec{b}|\sin\theta\vec{n}$$。其中，$|\vec{a}|$ 和 $|\vec{b}|$ 分别表示向量 $\vec{a}$ 和 $\vec{b}$ 的模长，$\theta$ 表示向量 $\vec{a}$ 和 $\vec{b}$ 之间的夹角（取 $0\leq\theta\leq\pi$），$\vec{n}$ 表示两向量所在平面的法向量，其大小为 $|\vec{n}|=|\vec{a}||\vec{b}|\sin\theta$。对于二维平面向量，其叉积运算可以用行列式表示：。$$\vec{a}\times\vec{b}=\begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix}=a_1b_2-a_2b_1$$。其中，$\begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix}$ 表示二阶行列式。
向量和平面相乘的公式是：。$\vec{a} \cdot (\vec{b} \times \vec{c}) = \vec{b} \cdot (\vec{c} \times \vec{a}) = \vec{c} \cdot (\vec{a} \times \vec{b})$。其中，$\vec{a}$，$\vec{b}$，$\vec{c}$ 分别为三维向量，$\times$ 表示向量的叉积，$\cdot$ 表示向量的点积。向量相乘的计算公式有两种：。1. 向量的点积计算公式：。$\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos{\theta}$。其中，$\theta$ 为 $\vec{a}$ 和 $\vec{b}$ 之间的夹角。2. 向量的叉积计算公式：。$\vec{a} \times \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \sin{\theta} \cdot \vec{n}$。其中，$\theta$ 为 $\vec{a}$ 和 $\vec{b}$ 之间的夹角，$\vec{n}$ 为垂直于 $\vec{a}$ 和 $\vec{b}$ 所在平面的单位向量，方向由右手法则确定。
向量和平面相乘公式：。- 两个向量的叉乘结果是一个平面向量，表示这两个向量所在的平面的法向量。- 平面向量的点积结果是一个标量，表示这个平面向量在与其垂直的方向的投影长度。平面向量与向量相乘公式：。- 点积结果是一个标量，表示向量在平面向量所在的平面上的投影长度。- 叉积结果是一个向量，表示向量在与其垂直的方向上的投影长度。
向量和平面相乘公式：。设 $ \boldsymbol{a}=(a_1,a_2,a_3) $ 是三维向量， $ \boldsymbol{n}=(n_1,n_2,n_3) $ 是平面的法向量，则 $ \boldsymbol{a} $ 在平面上的投影向量为：。$ \boldsymbol{P_{\boldsymbol{n}}\boldsymbol{a}}=\frac{\boldsymbol{a}\cdot\boldsymbol{n}}{\|\boldsymbol{n}\|^2}\boldsymbol{n} $。平面向量数量积公式：。设 $ \boldsymbol{a}=(a_1,a_2,a_3) $ 和 $ \boldsymbol{b}=(b_1,b_2,b_3) $ 是两个三维向量，它们在平面上构成一组基，则它们的数量积为：。$ \boldsymbol{a}\cdot\boldsymbol{b}=a_1b_1+a_2b_2+a_3b_3 $。其中， $ \boldsymbol{a} $ 和 $ \boldsymbol{b} $ 的数量积也可以写成 $ \boldsymbol{a}\cdot\boldsymbol{b}=\|\boldsymbol{a}\|\|\boldsymbol{b}\|\cos\theta $ 的形式，其中 $ \theta $ 是 $ \boldsymbol{a} $ 和 $ \boldsymbol{b} $ 之间的夹角。
向量和平面相乘公式：。1. 向量与标量相乘公式：k(a,b,c) = (ka,kb,kc)。2. 向量点积（内积）公式：a·b = |a||b|cosθ，其中θ为a和b的夹角。3. 向量叉积（外积）公式：a×b = |a||b|sinθn，其中n为a和b的法向量方向，|n| = 1。4. 三维向量混合积公式：(a×b)·c = a·(b×c)。5. 平面法向量公式：对于平面Ax + By + Cz + D = 0，其法向量为n = (A,B,C)。6. 平面点法式公式：对于平面上的一点P(x0,y0,z0)和其法向量n = (A,B,C)，平面的方程为Ax + By + Cz + D = 0，其中D = -(Ax0 + By0 + Cz0)。向量运算的所有公式：。1. 向量加法公式：a + b = (ax + bx, ay + by, az + bz)。2. 向量减法公式：a - b = (ax - bx, ay - by, az - bz)。3. 向量的模长公式：|a| = √(ax² + ay² + az²)。4. 向量单位化公式：a/|a|。5. 向量的投影公式：proj_b a = (a·b/|b|²)b。6. 向量的反投影公式：perp_b a = a - proj_b a。7. 向量的夹角公式：cosθ = (a·b)/(|a||b|)，其中θ为a和b的夹角。8. 向量的平行公式：a∥b ⇔ a = kb。9. 向量的垂直公式：a⊥b ⇔ a·b = 0。
向量和平面相乘公式：。1. 向量和向量的乘积：两个向量的乘积等于它们的长度的乘积再乘以它们夹角的余弦值，即：。$\vec{a}\cdot\vec{b}=|\vec{a}|\cdot|\vec{b}|\cdot\cos\theta$。其中，$\vec{a}$和$\vec{b}$是两个向量，$\theta$是它们的夹角。2. 向量和平面的乘积：一个向量和一个平面的乘积等于这个向量在平面上的投影长度乘以这个向量的长度，即：。$\vec{a}\cdot\vec{n}=|\vec{a}|\cdot|\vec{p}|\cdot\cos\theta$。其中，$\vec{a}$是一个向量，$\vec{n}$是一个平面法向量，$\vec{p}$是$\vec{a}$在平面上的投影向量，$\theta$是$\vec{a}$和$\vec{n}$的夹角。平面向量的乘法：。平面向量的乘法是指将两个平面向量进行数乘和向量积两种运算的过程。1. 数乘：两个平面向量的数乘等于对应分量的乘积之和，即：。$(a_{1},a_{2})\cdot k=(k\cdot a_{1},k\cdot a_{2})$。其中，$(a_{1},a_{2})$表示一个平面向量，$k$是一个实数。2. 向量积：两个平面向量的向量积是一个向量，它的大小等于两个向量围成的平行四边形的面积，方向垂直于这个平行四边形，满足右手定则，即：。$(a_{1},a_{2})\times(b_{1},b_{2})=(0,0,a_{1}b_{2}-a_{2}b_{1})$。其中，$(a_{1},a_{2})$和$(b_{1},b_{2})$是两个平面向量。
向量和平面相乘公式是空间向量运算中的一个重要公式，表示一个向量在平面上的投影。假设有一个平面方程为Ax + By + Cz + D = 0，向量P(x1,y1,z1)，则向量P在平面上的投影Q(x2,y2,z2)的坐标可以通过以下公式计算得出：。x2 = x1 - [(Ax1 + By1 + Cz1 + D)A / (A^2 + B^2 + C^2)]。y2 = y1 - [(Ax1 + By1 + Cz1 + D)B / (A^2 + B^2 + C^2)]。z2 = z1 - [(Ax1 + By1 + Cz1 + D)C / (A^2 + B^2 + C^2)]。其中，Ax + By + Cz + D = 0为平面的向量方程，A、B、C、D分别为平面方程中的常数项，(x1,y1,z1)为向量的坐标，(x2,y2,z2)为向量在平面上的投影坐标。这个公式的实际应用可以用来求解空间向量的垂直、平行分量，以及空间向量在平面上的投影等问题。
猜你喜欢
