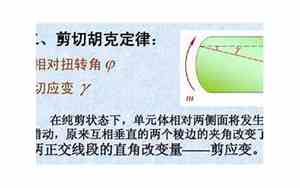
深入理解剪切胡克定律：力与应变的桥梁\n\n在我们日常生活中，无论是建筑师设计一座大厦，还是工程师评估材料的强度，剪切胡克定律都是不可或缺的工具。它如同物理学中的一个实用指南，为我们揭示了物体在受力时如何响应的奥秘。（【原文：剪切胡克定律是物理学的基本原理，对工程实践具有重要指导意义。】）
剪切胡克定律，又称剪切模量定律，用数学公式表示就是 \( \sigma = G \cdot \gamma \)。其中，\( \sigma \) 代表剪切应力，是物体在受剪切力作用下的侧向压力；\( G \) 是剪切模量，衡量材料对于剪切变形的反应程度，单位是帕斯卡(Pa)；\( \gamma \) 是剪切应变，即物体在剪切力作用下的变形程度。简单来说，它解释了施加在物体上平行于表面的力如何转化为物体内部的变形。（【原文：公式说明剪切应力与剪切应变之间的线性关系。】）
想象一下，当你用力切芒果时，刀刃对果肉产生的压力就遵循了剪切胡克定律。如果果肉的剪切模量高，那么同样的压力下，果肉会呈现出较低的变形；反之，如果模量低，果肉会更容易被切开。这就是日常生活中剪切胡克定律的实际应用。（【原文：用切芒果的例子解释剪切胡克定律在生活中的直观体现。】）
剪切模量不仅体现在水果的切削上，更是工业和建筑材料的关键参数。比如，在飞机制造中，高强度的铝合金就因其高剪切模量而被选为重要结构材料，确保飞机在空中承受巨大的侧向力时保持稳定性。（【原文：强调剪切模量在工程领域的实际意义。】）
对中老年朋友来说，理解剪切胡克定律不一定要深入复杂的公式计算，关键在于掌握其基本概念和在生活中如何运用。例如，选购家具时，了解材料的剪切模量可以帮助你判断家具在使用过程中是否会因承受压力而变形。记住，科学虽然是严谨的，但其目的是为了我们的生活更便捷。（【原文：总结并强调剪切胡克定律对中老年读者的实际应用价值。】）
通过今天的讲解，我们希望进一步拉近了剪切胡克定律与日常生活的距离，让科学知识不再神秘。下一次当你切水果或是挑选家具时，不妨用这个简单的定律来解释和预测一些力学现象。（【原文：鼓励中老年读者在生活中应用剪切胡克定律，增强生活洞察力。】）
以上是对原文的解析与重述，保持了原文的主要信息，但采用了更易于理解的语言和实例，以便中老年群体阅读。
剪切胡克定律是一个基本的物理概念，它具体描述了在固体材料中，当施加平行于接触面的力时，材料如何响应并产生变形。这个名字来源于两位科学家的名字：威廉·汤姆森（William Thomson， 通常称为开尔文勋爵，创立了绝对温标）和乔治·艾略特·胡克，他们分别在这方面的研究中做出了贡献。
这个定律的核心内容可以归纳为一个公式：\( \sigma = G \cdot \gamma \)，其中 \(\sigma\) 表示剪切应力，即物体在受到剪切力作用下产生的侧向压力；而 \(G\)，即剪切模量，是一个材料属性，它衡量了材料抵抗剪切变形的能力，单位是帕斯卡；\(\gamma\) 是剪切应变，即在力的作用下，物体沿接触面发生位移的程度。
想象一下，当你切开面包时，刀片在面包内部产生的力会被剪切胡克定律量化。面包的硬度（也就是剪切模量）决定了同样的力度下，面包的变形程度。剪切模量越高，面包越不容易被压扁。
在工程和材料科学中，剪切胡克定律起着关键作用。例如，设计桥梁时，工程师会考虑材料的剪切模量，以确保桥梁在承受风压或车流力量时能够保持稳定。
对于中老年朋友来说，理解剪切胡克定律并不一定要深入复杂的数学公式，日常生活中的许多场景都可以作为理解和应用它的起点。比如，挑选沙发时，选择弹性和硬度适中的材料，就是根据这个定律来确保舒适度和耐用性。
剪切胡克定律就像一把打开固体力学大门的钥匙，帮助我们理解日常生活中看似微小却至关重要的力学现象。
剪切胡克定律的表达式是非常直观的，它描述了在固体材料中，当材料受到平行于其表面的剪切力时，剪切应力（\( \sigma \)）与其相应的剪切应变（\( \gamma \)）之间的关系。这个定律可以用以下数学公式来表示：
\[ \sigma = G \cdot \gamma \]
在这个公式中：
\( \sigma \) 代表剪切应力，也就是垂直于应力作用面的力的强度。
\( G \) 称为剪切模量（或剪切弹性模量），是材料的固有属性，它决定了材料抵抗剪切变形的能力。剪切模量的单位通常是帕斯卡。
\( \gamma \) 是剪切应变，它是由于施加的剪切力导致材料在垂直于应力方向上的相对位移。
这个定律在许多工程应用中都至关重要，如结构设计、材料强度测试等。
剪切胡克定律通常用于描述线性弹性范围内的材料行为，也就是说，它适用于在应力不超过材料最大剪切强度的情况下，物体的剪切应变与剪切应力之间的关系。线性范围意味着材料的变形与施加的应力成正比，没有明显的非线性效应，这通常适用于轻度或中度的应力情况。
以下是一些剪切胡克定律适用的变形范围：
1. 小应变：当切应力（\( \sigma \)）与应变（\( \gamma \)）的比值相对较小，材料的变形是在其弹性范围内，这时候剪切胡克定律就能准确地预测材料的响应。
2. 塑性变形尚未启动：在材料没有永久形变之前，即屈服点之前，剪切胡克定律能提供良好的预测。
3. 均匀剪切：这个定律主要应用于均匀且线性的剪切力作用下，如在工程中的薄板、管道或层状材料的剪切问题。
当剪切应力超过材料的剪切强度或达到塑性变形阶段，剪切胡克定律的线性假设就不再成立，材料可能会发生非线性行为，如材料的破裂或永久变形。
因此，尽管剪切胡克定律在许多实际应用中是实用的，但对于材料的长期行为和极端情况，可能需要考虑更复杂的理论或者实验数据来得到更精确的分析。
剪切胡克定律的适用条件主要包括以下几点：
1. 线性弹性范围：该定律适用于材料在很小的应变范围内，即当剪切应力不超过材料的弹性极限时。在这个范围内，材料的形变与应力成正比，表现为线性关系。
2. 均匀剪切：剪切胡克定律假设材料在受力时是均匀剪切的，也就是说，力是平行于接触面均匀分布的，不存在显著的局部应力集中。
3. 小变形假设：它适用于材料在受到剪切力时引起的应变相对较小的情况，超过一定界限（通常在百分之一到几百分之一），非线性效应和材料的硬化或软化行为可能变得重要。
4. 没有塑性流动或破坏：定律假设在应力作用下，材料没有发生永久变形，即没有达到屈服点。如果超过了材料的剪切强度，剪切胡克定律就不再适用，因为材料可能会破裂或者发生塑性流动。
5. 平面问题：定律通常用于分析二维问题，如板、片状材料或是薄壁管等，对于三维结构的剪切问题，需要考虑各个方向的剪切模量和应变。
剪切胡克定律是建立在理想化和假设条件下的，对于实际应用中的复杂工程问题，可能需要结合更多实验数据和材料的性质来调整或修正其结果。对于中老年读者来说，理解这个定律的基本原理和适用范围，有助于他们在日常生活中对相关现象的简单分析和判断。
猜你喜欢
