面面相交的性质定理如何证明

在数学中，面与面相交是一个非常重要的概念。它涉及到几何图形的交叉和相交的性质。当两个面相交时，会出现一些有趣的现象和规律。本篇文章将以面与面相交的性质为主题，深入探讨面与面相交的现象和规律，以及它们的应用。

首先，让我们来看一下面与面相交的一般性质。当两个面相交时，它们形成了一条线，这条线称为交线。交线的性质非常重要，因为它可以帮助我们理解面与面相交时的交叉关系。交线可以是直线，也可以是曲线。如果两个面相交于一条直线，那么它们就是平面交。如果两个面相交于一条曲线，那么它们就是曲面交。无论是平面交还是曲面交，它们的相交性质都是相似的。

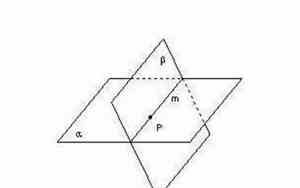
接下来，我们来研究一下面与面相交的几个特殊情况。第一种情况是两个平面相交。当两个平面相交时，它们形成了一条直线。这条直线是它们的交线。交线与两个平面的法向量垂直，这也就是说，交线同时也是两个平面的法线。如果两个平面相互平行，那么它们的交线为无穷远处的直线。此时，两个平面是没有交点的。

第二种情况是一个平面和一个曲面相交。平面和曲面的交线可以是一个点，也可以是一条曲线。当交线为点时，平面与曲面交于一个点；当交线为曲线时，平面与曲面交于一个曲线。交线的形状和位置取决于曲面的形状和位置。

第三种情况是两个曲面相交。两个曲面相交时，它们的交线可以是一条直线，也可以是一条曲线。当交线为直线时，曲面相交形成了一个切平面；当交线为曲线时，曲面相交形成了一个切曲线。交线可以是弧、圆等曲线。

接下来，我们来讨论一下面与面相交的应用。面与面相交在很多领域都有着广泛的应用，例如建筑、机械、图形学等。我们以建筑为例来说明。

在建筑中，面与面相交的问题是非常常见的。建筑师在设计建筑物时，需要考虑建筑物中各种不同形状和大小的立面之间的相交关系。例如，在设计一个圆形建筑时，需要考虑圆形墙面如何与其他直线型墙面相交。此时，建筑师需要运用面与面相交的知识，来计算相交的面积和建筑的结构。

此外，在机械制造中，面与面相交的问题也是非常重要的。例如，在设计一台机器时，需要考虑机器中各种不同形状和大小的零件之间的相交关系。此时，工程师需要使用面与面相交的知识，来计算零件之间的相交面积和接触点的位置。

总之，面与面相交是一个非常重要的数学概念。它涉及到几何图形的相交和交叉的性质，是很多领域都必须要掌握的基本知识。我们可以通过学习面与面相交的性质，来提高对几何图形的理解和认识，进而运用到实际问题中。

两个面相交知识点

1. 相交线：两个面相交所形成的线称为相交线，相交线在两个面上都存在。2. 角度：两个面相交所形成的角度称为交角度，交角度是两个面的法线的夹角。3. 相交部分：两个面相交所形成的部分称为相交部分，相交部分可以是线段、平面或者体积。4. 平行面：如果两个面相交的交线与另一面平行，则这两个面互相平行。5. 垂直面：如果两个面相交的交线与另一面垂直，则这两个面互相垂直。6. 角平分线：如果两个面相交的交线是一条角平分线，则这两个面的夹角相等。7. 交点：两个面相交所形成的点称为交点，交点在两个面相交的交线上。8. 夹角大小：两个平面的夹角大小等于它们法线的夹角大小。9. 交线性质：两个平面相交的交线与任意一平面垂直。10. 平面平移：两个平面的相交线不随着平面平移而发生变化，交点也不随着平移而改变。

面面相交的判定

1. 平面相交定理：如果两个平面不平行，那么它们一定相交。2. 垂直面相交定理：如果两个平面相交，且其中一面是另一面的垂直平面，那么它们相交线一定是它们的交线。3. 平行面相交定理：如果两个平行平面相交，那么它们的交线是一条平行于这两个平面的直线。4. 倾斜面相交定理：如果两个倾斜的面相交，那么它们的交线是一条不在它们的共面内的直线。5. 平面的位置关系：当两个平面相交时，它们的位置关系有三种可能：交于一点、交于一条直线、没有交点。6. 空间中平面的交线：两个平面的交线可能是一条直线、两条平行直线或没有交线。

面与面的交线有什么性质

面与面相交的性质：。1. 相交处的点位于两个面的交线上。2. 两个面的交线在相交处正交于两个面的法线。3. 两个面的交线是两个平面的公共部分，因此它本身也是一条平面。面与面的交线有什么性质：。1. 交线是两个面的公共部分，因此交线上的点都位于这两个面上。2. 交线在两个面上的投影都是直线。3. 交线被两个面所包含，因此交线的长度等于两个面相交时的面积。

什么叫面与面相交

面与面相交指两个或多个平面相交，即在空间中有共同的交线段或交点。当两个平面相交时，它们形成一个共同的边界线，这个边界线被称为交线。交线和交点是面与面相交的重要性质，它们可以用来计算角度、距离和面积等几何量。

空间中面与面相交得

到一个直线或一个平面，这取决于两个面的相对位置和方向。如果两个面相交，但是它们的交线不在其中一个面上，那么它们是斜交的。如果两个平面完全重合，那么它们交集是整个平面。同时，两个平面可以平行，这意味着它们永远不会相交。

面与面相交成什么

当两个平面相交时，它们会形成一条直线，称为它们的交线。此外，它们还有以下性质：。1. 相交平面必定共线；。2. 相交平面的交线垂直于两个平面的法线；。3. 两个平面的交线只有在它们不互相平行时才存在；。4. 如果两个平面的交线存在，则它们的交线是无限延伸的。总之，当两个平面相交时，它们形成的是一条无限延伸的直线。

面与面相交得到

线或点。当两个平面相交时，它们的交线是在两个平面上的一条公共直线。如果两个平面不平行，则它们相交于一条直线。如果两个平面平行，则它们永远不会相交。如果两个平面相交于一个点，则该点在两个平面上都是公共点。这个点也可以看做是两个平面的交点。在三维空间中，如果两个平面相交于一个直线，则该直线在两个平面上都是公共的。该直线也可以看做是两个平面的交线。平面的相交关系在计算几何、立体几何以及工程学等领域有着广泛的应用。

两平面相交有什么性质啊

两平面相交会产生一条直线，这条直线被称为交线或交集线。交线相交于两个交点，这两个交点在两个平面上均存在。同时，两个平面相交也满足以下性质：。1. 两平面相交于一条直线，这条直线平行于两平面的法线。2. 两平面相交角度的大小等于它们法线的夹角。3. 两个互相垂直的平面相交，交线垂直于这两个平面。4. 两个平面相交的交线不一定是直线，它们也可能是一些曲线或曲面。5. 如果两个平面相交的角度是锐角，则它们必相交于一条直线以上。6. 如果两个平面相交的角度是钝角，则它们必相交于一条直线以下。7. 如果两个平面不相交，则它们的交集为空集。