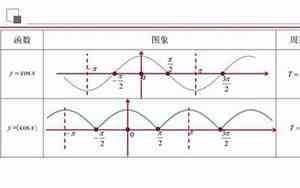
三角函数的周期性是它们最显著的特性之一，根据其定义和性质，主要有两种主要的周期函数：正弦函数和余弦函数。
1. 正弦函数（sin(x)）周期：
正弦函数的周期是 \(2\pi\)，也就是说，对于任何实数 \(x\)，\(\sin(x + 2\pi) = \sin(x)\)。这是因为正弦的波形在一个完整的圆周（2π单位）后回到初始位置。
2. 余弦函数（cos(x)）周期：
余弦函数的周期同样是 \(2\pi\)，\(\cos(x + 2\pi) = \cos(x)\)。余弦函数的波形也随着角度增加 \(2\pi\) 周期性地重复。
对于其他三角函数，比如正切函数，它的周期是 \(\pi\) 因为 \(\tan(x + \pi) = \tan(x)\)。余切、正割和余割的周期则分别是 \(π\) 的整数倍。
这些都是基本的周期公式，这些周期性在解决实际问题和理论研究中非常重要，它们可以帮助我们理解和预测函数的行为。如果需要更详细的信息或者特定的三角函数周期公式，欢迎指出！
三角函数的周期性公式通常根据它们的定义来确定，以下是一些常见的三角函数及其周期性：
1. 正弦函数（\(\sin(x)\)）：
周期 \(T = 2\pi\)，因为 \(\sin(x + 2\pi n) = \sin(x)\) 对于任何整数 \(n\)。
2. 余弦函数（\(\cos(x)\)）：
周期 \(T = 2\pi\)，因为 \(\cos(x + 2\pi n) = \cos(x)\)。
3. 正切函数（\(\tan(x)\)）：
周期 \(T = \pi\)，因为 \(\tan(x + \pi n) = \tan(x)\)。对于有理数 \(n\)，会形成多个小周期。
4. 余切函数（\(\cot(x)\)）：
周期 \(T = \pi\)，因为 \(\cot(x + \pi n) = \cot(x)\)。正切的倒数，所以周期相同。
5. 正割函数（\(\csc(x)\)）：
正割是正弦的倒数，所以周期 \(T = 2\pi\)，\(\csc(x + 2\pi n) = \csc(x)\)。
6. 余割函数（\(\sec(x)\)）：
余割是余弦的倒数，所以周期 \(T = 2\pi\)，\(\sec(x + 2\pi n) = \sec(x)\)。
上述公式说明了三角函数在同一周期内的重复性质。在实际应用中，知道周期可以帮助我们分析函数在不同角度或时间上的周期性特征。如果需要特定的周期公式或者说明，欢迎继续提问。
周期函数的八个基本公式通常指的是正弦、余弦、正切、余切、正割和余割函数的一些基本周期性质。以下是这些函数的基本周期公式：
1. 正弦函数 \(\sin(x)\)
周期 \(T = 2\pi\)，因为 \(\sin(x + 2\pi n) = \sin(x)\) （\(n\) 是整数）。
2. 余弦函数 \(\cos(x)\)
周期 \(T = 2\pi\)，因为 \(\cos(x + 2\pi n) = \cos(x)\)。
3. 正切函数 \(\tan(x)\)
周期 \(T = \pi\) （基本周期），因为 \(\tan(x + \pi n) = \tan(x)\)。
4. 余切函数 \(\cot(x)\)
周期 \(T = \pi\)，因为它是 \(\tan(x)\) 的倒数，\(cot(x + \pi n) = \cot(x)\)。
5. 正割函数\(\csc(x) = \frac{1}{\sin(x)}\)：
周期 \(T = 2\pi\)，因为 \(\csc(x + 2\pi n) = \csc(x)\)。
6. 余割函数\(\sec(x) = \frac{1}{\cos(x)}\)：
周期 \(T = 2\pi\)，因为 \(\sec(x + 2\pi n) = \sec(x)\)。
请注意，这些函数在定义域内并不总是完全周期的，如正切函数在 \(\tan\) 的定义域中，\(x + \pi\) 是基本周期。若要在有限区间内研究这些函数，可能需要更具体分析。
如果你需要关于某个特定的三角函数的详细周期性，或者有其他数学问题，欢迎继续提问！
周期函数的推导主要基于它们的定义和性质。在三角函数中，周期性源于角度的重复。以下是每个基本三角函数的周期性推导：
1. 正弦函数 \(\sin(x)\)：
因为正弦函数定义为对任意角 \(x\) 的单位半圆的对边与斜边的比例，其波形是一个完整的半圆。从 \(x\) 到 \(x + 2\pi\)，角度走了整个圆周，所以对边重复了，因此 \(\sin(x + 2\pi n) = \sin(x)\) 对所有整数 \(n\) 都成立，周期为 \(2\pi\)。
2. 余弦函数 \(\cos(x)\)：
同理，余弦函数是半圆的邻边与斜边的比例，半圆后余弦值不变，\(\cos(x + 2\pi n) = \cos(x)\)，周期也为 \(2\pi\)。
3. 正切函数 \(\tan(x)\) 和 \(\cot(x)\)：
正切是正弦与余弦的比值，\(\tan(x + \pi) = \frac{\sin(x + \pi)}{\cos(x + \pi)} = \frac{-\sin(x)}{-\cos(x)} = \tan(x)\)，所以周期是 \(\pi\)。余切是正切的倒数，所以周期相同。
4. 正割函数 \(\csc(x)\) 和 \(\sec(x)\)：
正割是 \(\csc(x) = \frac{1}{\sin(x)}\)，正弦的倒数，所以周期和正弦相同，为 \(2\pi\)。余割是 \(\sec(x) = \frac{1}{\cos(x)}\)，周期也是 \(2\pi\)。
以上推导都是基于函数的定义和三角形的性质，是直观的理解。在严格证明上可能涉及复数域的分析，但这里概述的版本对于理解基本概念已经足够。
三角函数的周期性和对称性是它们在数学分析中的两个重要特性：
1. 周期性：
正弦函数（\(\sin(x)\)） 和 余弦函数（\(\cos(x)\)）：这两种函数的周期是 \(2\pi\)。这意味着，对于任何 \(x\)，在 \(x\) 增加 \(2\pi\) 之后，它们的值会回到原来的值。例如，\(\sin(x + 2\pi) = \sin(x)\) 和 \(\cos(x + 2\pi) = \cos(x)\)。
正切函数（\(\tan(x)\)），余切函数（\(\cot(x)\)），正割（\(\csc(x)\)）和余割（\(\sec(x)\)）：它们的周期取决于它们是以什么为基础定义的，如正切和余切的周期是 \(π\)，而正割和余割的周期是 \(2\pi\)。
2. 对称性：
正弦函数：正弦函数是对称的，但不是关于原点，而是关于 \((\frac{\pi}{2}， 0)\) 和 \((- \frac{\pi}{2}， 0)\) 这两条对称轴。它在每个完整周期内只有一个最大值和一个最小值。
余弦函数：余弦函数也是对称的，有一个对称轴在每个 \(x = n\pi\)（\(n\) 是整数），关于这些轴的奇数倍数点，余弦值是 1 或 -1。
正切和余切：正切和余切函数在每一个 \(\pi\) 倍数的点是奇函数，它们的图形关于这些点是对称的。
正割和余割：正割函数有对称轴 \(x = \pm n\pi\)，余割函数则有对称中心 \(x = n\pi\)。
理解这些周期性和对称性对于解决三角函数问题、图形分析以及物理和工程问题中的波形处理至关重要。
三角函数的周期性主要与它们定义的基础有关，最小正周期通常指的是一个函数绕其基本结构旋转一周所需的最小角度。
1. 正弦函数（\(\sin(x)\)） 和 余弦函数（\(\cos(x)\)）：
它们的最小正周期是 \(2\pi\)。这意味着当你向右移动 \(2\pi\) 角度，函数的图形会回到起始位置，重复其周期性。这是所有基于圆周的三角函数的基本周期。
2. 正切函数（\(\tan(x)\)）和余切函数（\(\cot(x)\)）：
最小正周期是 \(\pi\)，这是因为正切函数是正弦和余弦比值，当角度增加 \(\pi\) 时，比值保持不变，图形完成一个周期。
3. 正割函数（\(\csc(x) = \frac{1}{\sin(x)}\)）和余割函数（\(\sec(x) = \frac{1}{\cos(x)}\)）：
由于它们是倒数关系，它们的最小正周期与它们的基础函数相同，即 \(2\pi\) 和 \(2\pi\)。
最小正周期的概念在解决周期性问题或解析图形时非常重要，因为它可以帮助我们确定函数在多大范围内重复自身。例如，在信号处理或物理问题中，识别周期可以用来预测或分析重复的模式。
猜你喜欢
