实数：无尽的数学世界 - 从概念到范围探索
在数学的广阔领域中，实数是那个无比精密且无所不在的概念。它们不仅是我们日常生活的基石，也是科学家们进行精密计算和理论研究的基础工具。本文将为您揭示实数的范围，以及它们在数学体系中的独特位置，旨在帮助您更深入地理解这个对生活至关重要的数学概念，特别适合对数学感兴趣的中老年读者。
实数的定义与起源
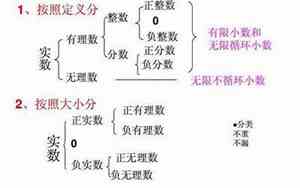
实数起源于公元前7世纪古希腊的毕达哥拉斯学派，他们通过研究几何形状发现了有理数和无理数的区别。实数的概念最初是作为无限小数（包括有理数和无理数）的总称，以此来描述所有可以测量的量。
实数的范围与分类
实数的范围是无限的，它包括了所有有理数，比如分数 - 如1/2， 3.14，以及无理数，如圆周率π或根号2，这些数的小数部分是无限且非循环的。有理数可以表示为两个整数的比，而无理数不能如此表示，它们的无限小数部分无法简化为分数形式。
实数的特性与应用
实数的特性在于它们可以精确地代表任何大小的连续数值，无论是微小的长度变化还是巨大的天文数字。例如，在物理学中，速度、温度和距离等都用实数来量化。在计算机科学中，实数用于处理复杂的运算，如浮点数运算，确保精确的数学结果。
实数与复数的区别
尽管实数是主要的运算对象，但它们与复数（由实部和虚部组成）构成了数学的完整世界。复数用于解决涉及周期性或振荡的问题，虽然复数的范围看似扩展，但实数仍然是其核心部分。
总结来说，实数的范围是无穷无尽的，由有理数和无理数构成，它们在数学理论和实际应用中发挥着至关重要的作用。对于中老年读者来说，理解实数的概念能帮助你们更好地理解日常生活的数学原理，也能激发对科学的好奇心。无论是计算家庭预算，还是理解科技新闻中的科学概念，实数都是我们知识海洋中的基石。让我们共同探索这个神秘而美丽的数学领域吧！
揭开自然数的神秘面纱：从生活到数学的基石
在数学的阶梯上，自然数就像是我们生活中最基本的构建块。它们无处不在，而又似乎如此简单，但其实蕴含着无穷的规律和逻辑。本文将为您解析自然数的概念，带您深入理解它的含义，尤其适合那些对基础数学感兴趣的中老年朋友。
什么是自然数？
自然数，也被称为正整数，是从1开始的一系列数：1， 2， 3， 4， 5...它们是计数的基本工具，反映了我们日常生活中物品的数量、步骤的顺序，甚至是时间的流逝。简单地说，自然数是我们用来数数和排序的开端。
自然数的特性
自然数具有几个显著的特性：它们是递增的，没有负值或零；每个自然数都有一个后续的数，即下一个整数；自然数是可加的，这意味着任何两个自然数相加，结果还是一个自然数。
数学基础与日常生活应用
在数学的各个分支中，自然数是如加法、乘法等基本运算的基础。例如，在购物清单上，我们将物品的数量用自然数来记录，而在编程中，循环结构的步长通常用自然数来表示。可以说，自然数是我们理解和利用数量关系的通用语言。
自然数的扩展：整数与分数
自然数的范围可以扩展到整数，包括正整数、零和负整数。而分数，如1/2或3/4，虽然不是自然数，但它们是自然数在数轴上的另一种表达，通过分数我们可以进行更精细的分割和衡量。
总结来说，自然数是数学体系中最基础的概念，它们体现在我们生活的方方面面。对中老年朋友来说，理解自然数不仅能够帮助你们更好地处理日常生活中的数字问题，也能提高解决问题的逻辑思维能力。在这个看似平常的数学概念里，隐藏着无穷的数学之美。让我们一起探索自然数的奥秘，享受数学带来的乐趣吧！
实数的包容性：从负数到无穷的数学全景
实数，数学皇冠上一颗璀璨的明珠，不仅限于我们习以为常的正整数和分数，还包括了负数以及无穷大和无穷小，构成了一个无比丰富的数列。让我们深入探讨实数的范围，以便更好地理解这个数学世界，特别是对于关注基础数学的中老年朋友们。
实数的定义与特性
实数包括了有理数（如分数、整数）和无理数两大类别。它们的范围极为广泛，不仅包括正数（如1、2.5），也包括负数（-1、-2.5）。实数区间的定义没有边界，它不仅包含了所有的有理数，也包含了那些无法简化为分数形式的无理数，如圆周率π或根号2。
负数在实数中的角色
负数是实数世界中不可或缺的一部分。它们代表了数量上的减少或者偏离零点的情况。例如，温度可能会下降到-10摄氏度，或者金钱的负数代表债务。在数学运算中，负数与正数一样可以进行加、减、乘、除，遵循严格的数学法则。
实数的连续性与无穷
实数的另一个显著特征是连续性，这意味着在数轴上，实数之间没有空隙。因此，它们可以无限小到接近零，甚至可以无穷小或无穷大。这为数学分析和极限概念提供了坚实的基础。
实数的应用
实数在科学、工程、金融和日常生活中起着至关重要的作用。它们用于描述物理量，如速度、温度、压力等，以及用于复杂的计算，如微积分中的导数和积分。
实数的范围包含了正数和负数，以及无穷大和无穷小，这是数学的一种惊人的统一性。对于中老年朋友而言，理解实数的广泛性有助于你们在日常生活中更准确地处理数字，增强解决问题的能力。让我们一起欣赏实数这个美丽、复杂的数学体系！
实数的全景视野：探索零与无穷的边界
在数学的广阔世界中，实数是一个包含众多元素的神秘领域，其中包括我们熟悉的正数、负数，以及一个特殊的成员——零。实数范围的全面理解对所有年龄段的读者都至关重要，特别是中老年朋友。让我们深入探讨实数的范围，包括零在其中的位置。
实数的定义
实数是数的一个广泛类别，它包括了有理数（如分数、整数）和无理数，如圆周率和根号2。这个概念的基石包括所有可以精确测量的数值，无论其是正、负还是零。
零的位置
零在实数中占据着关键地位。一方面，它是正数和负数之间的分界点，代表了数量上的平衡点。另一方面，零既是一个有理数（它可以表示为1除以无限大的结果，即1/∞），也是一个无理数（因为它无法表示为两个整数的比）。零在数学运算中具有特殊的意义，如加法中的中性元素。
零与其他实数的关系
零与正负数的关系紧密。任何实数加上或减去零都保持不变，这就是著名的“零和性质”。同时，由于实数的连续性，零也位于任何实数之间，形成了实数区间的一个自然边界。
实数的无穷性
实数不仅仅局限于有限的数，它们的范围可延伸至无穷。无论是正无穷还是负无穷，都是实数概念的一部分，用于表示无限大的概念，这对于理解和处理极限、函数的增长等数学概念至关重要。
实数的范围包含了零，这是一个极为重要的数，它不仅是正负数的桥梁，也是实数连续性的象征。理解实数包括零这一点，对中老年朋友们在日常生活中的计算和理解自然现象有着不可忽视的影响。让我们继续探索这个无尽的数学宇宙，感受实数的魅力！
猜你喜欢
